Corresponde a una figura geométrica tridimensional, es decir, que se proyecta en tres dimensiones: largo, ancho y alto. Debido a esta característica existen en el espacio pero se hallan limitados por una o varias superficies.
Si todas las superficies que lo limitan son planas y de contorno poligonal, el cuerpo es un poliedro. (Ver Elementos de un poliedro).
Los poliedros se clasifican en regulares e irregulares.
 |
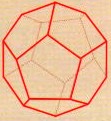Poliedros regulares, son aquellos cuyas caras son todas polígonos regulares, congruentes entre sí (de igual medida) y cuyos ángulos poliedros son iguales. Existen solamente 5 poliedros regulares: Tetraedro, Hexaedro, Octaedro, Dodecaedro,Icosaedro.
Para los geómetras griegos, el estudio de los poliedros fue muy importante y conocieron la existencia de esos cinco únicos sólidos regulares, cuyo descubrimiento atribuyeron algunos al propio Pitágoras y a los que Platón recurrió incluso para explicar la creación del universo. Sin embargo, no consta que conocieran un importante resultado relativo al número de vértices, aristas y caras de un poliedro convexo, observado ya por Descartes en 1640 y del que el matemático suizo Leonhard Euler dio una famosa demostración en 1752. Euler demostró que, si se suma el número de caras y el número de vértices de un poliedro convexo y, del valor obtenido, se resta entonces el número de aristas, et resultado es siempre igual a 2. De este resultado, válido para todo poliedro convexo, se deduce fácilmente la existencia de únicamente cinco poliedros regulares.
El cubo(:
Un cubo o hexaedro regular es un poliedro de seis caras cuadradas congruentes, siendo uno de los llamados sólidos platónicos.
Un cubo, además de ser un hexaedro, puede ser clasificado también como paralelepípedo, recto y rectángulo, pues todas sus caras son de cuatro lados y paralelas dos a dos, e incluso como un prisma de base cuadrangular y altura equivalente al lado de la base.
El hexaedro regular, al igual que el resto de los sólidos platónicos, cumple el Teorema de poliedros de Euler, pues tiene seis caras, ocho vértices y doce aristas (8+6=12+2).
La esfera(:
En geometría, una superficie esférica es una superficie de revolución o el conjunto de los puntos del espacio cuyos puntos equidistan de otro interior llamado centro. Los puntos cuya distancia es menor que la longitud del radio forman el interior de la superficie esférica. La unión del interior y la superficie esférica se llama esfera.
La esfera, como sólido de revolución, se genera haciendo girar una superficie semicircular alrededor de su diámetro (Euclides, L. XI, def. 14).
Esfera proviene del término griego σφαῖρα, sphaîra, que significa pelota (para jugar).Coloquialmente hablando, se emplean palabras como bola, globo (globo terrestre), etc., para describir un volumen esférico.
La piramide(:
No hay comentarios:
Publicar un comentario